GACE Program Admission Mathematics Subtest
You will have 1 hour and 30 minutes to answer 56 multiple-choice questions.
The Mathematics subtest can be neatly divided into three sections:
- Number and Quantity (36%)
- Data Interpretation and Representation, Statistics, and Probability (32%)
- Algebra and Geometry (32%)
Number and Quantity
This section tests your knowledge of ratio concepts, proportional relationships, the multiplication and division of fractions, and rational numbers. You will be asked to work with both radicals and integer exponents, to use quantitative reasoning to solve problems, and to find common factors and multiples.
Let’s discuss some concepts that will more than likely appear on the test.
Dividing Fractions by Fractions
When presented with a question that asks you to divide one fraction by another fraction, keep in mind that dividing fractions is just multiplying with reciprocals (reverse). Once your multiplication problem is set up, you will multiply your numerators then your denominators.

Integer Exponents
Remember that an exponent is the power to which a number is raised. For example, 43 is the same as 4 x 4 x 4. In this example, 3 is the exponent.
What might this look like on the test? You may, for example, be asked to compare two base/exponent combinations (such as 44 and 63) and decide which of the two is greater or if they are equivalent.
Common Factors and Multiples
To prepare for this section of your test, you should review both common factors and multiples, including least common multiples (LCMs) and greatest common factors (GCFs). The LCM of two numbers is the smallest number, excluding zero, that is a multiple of both numbers. The GCF is the greatest factor that can be used to divide two numbers. In order to determine the GCF of two numbers, list the prime factors of each of the two numbers. Then, multiply the prime factors which the numbers have in common in order to find your answer.
On the test, you may be asked to determine the greatest common factor of 18 and 24 (which is 6).
To prepare for this section of your test, you should review both common factors and multiples, including least common multiples (LCMs) and greatest common factors (GCFs). The LCM of two numbers is the smallest number, excluding zero, that is a multiple of both numbers. The GCF is the greatest factor that can be used to divide two numbers. In order to determine the GCF of two numbers, list the prime factors of each of the two numbers. Then, multiply the prime factors which the numbers have in common in order to find your answer.
On the test, you may be asked to determine the greatest common factor of 18 and 24 (which is 6).
Data Interpretation and Representation, Statistics, and Probability
This section tests your ability to work with data, solve measures of central tendency and spread problems, as well as identify data relationships in order to make predictions. You need to know the difference between correlation and causation and solve simple probability problems.
Let’s discuss some concepts that will more than likely appear on the test.
Measures of Center
The Mathematics test will require you to work with measures of central tendencies, such as mean, median, and mode. For example, take a look at the following question:
This list shows the price of jackets in a store last month: $34, $45, $46, $48, $56
This is the current list of jacket prices: $4, $45, $44, $48, $56
In the second list, which price is the outlier? Does the outlier change the mean, the median, or the mode?
In this example, the $4 price is the outlier, because it is drastically different from the other prices. The outlier does not affect the mode (frequency of appearance) of the prices. It also does not affect the median (midpoint) price, because the number of prices remains the same on both lists. It does, however, affect the mean (average) price. The mean price of the jackets in the first list is $45.80, and the mean price of jackets in the second list is $39.40. You can find the mean of each list by adding the price of each jacket and then dividing the sum by the number of items in the list (5).
Distributions
In statistics, a probability distribution is used to describe the likelihood of an outcome.
A discrete probability distribution may appear as a formula or a table listing all values that a discrete variable could be. Discrete variables have a finite and countable number of values and continuous variables do not.
Cumulative probability distributions describe the probability that the value of a variable will fall within a specific range.
A uniform probability distribution describes a situation in which every value of a random variable has an equal chance of occurring. For example, flipping a coin would have a uniform probability distribution. Each of the two outcomes (heads or tails) is equally likely to occur. Here’s an example.
Imagine that you will flip a coin twice.
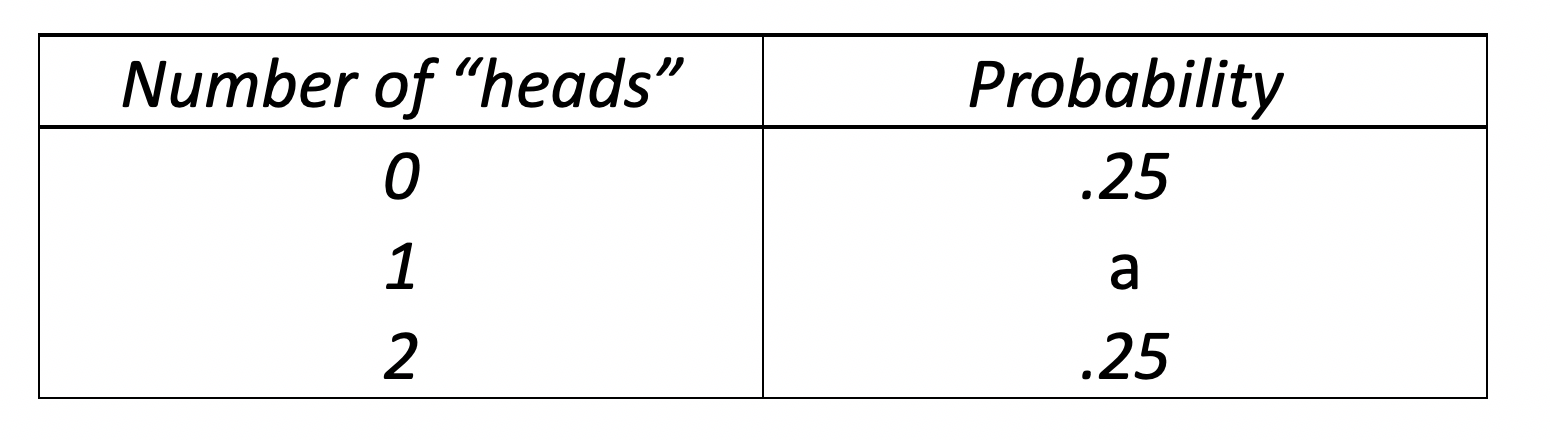
What value would correctly replace a in the distribution table?
The value .5 would correctly replace a because the probability values would then equal 100%.
Algebra and Geometry
This section tests your ability to solve algebraic problems, including linear and quadratic equations.
You also need to be able to recognize basic properties of two-dimensional shapes, as well as understand the concepts of congruency, similarity, area, circumference, and perimeter.
Here are some concepts that you may see on the test.
Solving for x
While completing the Algebra and Geometry portion, you’ll need to work with some variables. Variables don’t have to be scary! Just remember that a variable is a stand-in for a number. Most variables are represented with letters, like “x.”
You’ll be asked to solve equations to find out the value of variables. Here’s an example of the type of problem that you might find in this section of the test:
Solve for x:
4x – 2 = 2x + 8
To solve this equation, you would bring like terms to one side:
4x – 2x = 2 + 8
Add and subtract on each side:
2x = 10
And divide each side by 2 to find the value of x:
x = 5
Equivalent Expressions
Equivalent expressions have the same solution, but they may be written differently. To solve for equivalent expressions, you’ll need to combine like terms and use the distributive property. Just remember that the distributive property will require you to use the order of operations to find the correct answer!
Here’s an example of two equivalent expressions:
2x4 + 2x and 2(x4 + x).
The second example has the same value as the first. If you just distribute the 2 in the second equation, it will look like the first equation.
Geometrical Figures
This section tests your ability to solve algebraic problems, including linear and quadratic equations.
You also need to be able to recognize basic properties of two-dimensional shapes, as well as understand the concepts of congruency, similarity, area, circumference, and perimeter.
Here are some concepts that you may see on the test.
Solving for x
While completing the Algebra and Geometry portion, you’ll need to work with some variables. Variables don’t have to be scary! Just remember that a variable is a stand-in for a number. Most variables are represented with letters, like “x.”
You’ll be asked to solve equations to find out the value of variables. Here’s an example of the type of problem that you might find in this section of the test:
Solve for x:
4x – 2 = 2x + 8
To solve this equation, you would bring like terms to one side:
4x – 2x = 2 + 8
Add and subtract on each side:
2x = 10
And divide each side by 2 to find the value of x:
x = 5
Equivalent Expressions
Equivalent expressions have the same solution, but they may be written differently. To solve for equivalent expressions, you’ll need to combine like terms and use the distributive property. Just remember that the distributive property will require you to use the order of operations to find the correct answer!
Here’s an example of two equivalent expressions:
2x4 + 2x and 2(x4 + x).
The second example has the same value as the first. If you just distribute the 2 in the second equation, it will look like the first equation.
You need to know about parallel and perpendicular lines, as well as geometrical figures, including circles, quadrilaterals, and triangles. While you complete this portion, you will be asked to compare figures and to describe the relationships between them. You’ll also identify examples of congruence and interact with coordinate planes.
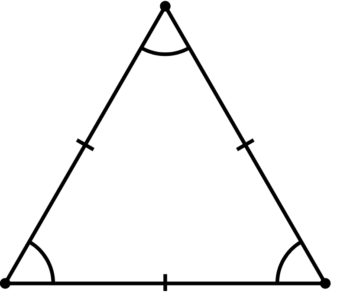
Here’s an example question (with answer) regarding a geometrical figure:
The given figure is a(n) equilateral triangle because each of its angles measures 60°.
Volume
Volume is how much space an object takes up. You’ll use your knowledge of volume formulas to solve problems like the one below:
Your neighborhood swimming pool is 30’ wide and 35’ long. It measures 6’ in depth. When filled to capacity, what is the volume of the pool? To solve this problem, think of the pool as a rectangular prism. To find the volume of a rectangular prism, all you need to do is multiply the length, width, and height:
V = l x w x h 30 x 35 x 6 = 6,300
The volume of the pool is 6,300 cubic feet.
Pythagorean Theorem
Questions about the Pythagorean theorem will test your knowledge of right triangles and your ability to use these shapes to solve equations, make comparisons, and draw conclusions.
According to this theorem, side c is the side of the triangle opposite the right angle; side a and side b are the other two sides of the right triangle. You will use the Pythagorean equation (a2 + b2 = c2), to solve related questions. Here’s an example of what a related question might look like on the test:
A piece of paper has been folded into a right triangle. Side a is 4 inches and side b is 3 inches. If side c is the hypotenuse, what is the length of side c?
To solve this problem, just plug the numbers into the Pythagorean equation:
42 + 32 = c2
Apply the exponents:
16 + 9 = c2
Add the values on the left:
25 = c2
And find the square root of c:
5 = c
So, the hypotenuse of the little origami craft must be 5 inches!
