TExES Physical Science 6-12 (237) Practice Test and Prep

Physical Science 6-12 (237) Practice Test

Preparing to take the TExES Physical Science 6-12 (237) exam?

Awesome!

Welcome to our TExES Physical Science 6-12 practice test and prep page. On this page, we outline the domains and key concepts for the Physical Science 6-12 exam. It is a free resource we provide so you can see how prepared you are to take the official exam.

While this free guide outlines the competencies and domains found on the exam, our paid TExES Physical Science 6-12 study guide covers EVERY concept you need to know and is set up to ensure your success! Our online TExES Physical Science 6-12 study guide provides test-aligned study material using interactive aids, videos, flash cards, quizzes and practice tests.

Will I pass using this free article? Will I pass using your paid study guide?

If you use this guide and research the key concepts on the TExES Physical Science 6-12 on your own, it’s possible you will pass, but why take that chance? With our paid study guide, we guarantee you will pass.

Quick Links to Help You Navigate This Page

• TExES Physical Science 6-12 (237) Information
• TExES Physical Science 6-12 Domain I: Scientific Inquiry and Processes
• TExES Physical Science 6-12 Domain II: Physics
• TExES Physical Science 6-12 Domain III: Chemistry
• TExES Physical Science 6-12 Domain IV: Science Learning, Instruction, and Assessment

TExES Physical Science 6-12 Information

Overview

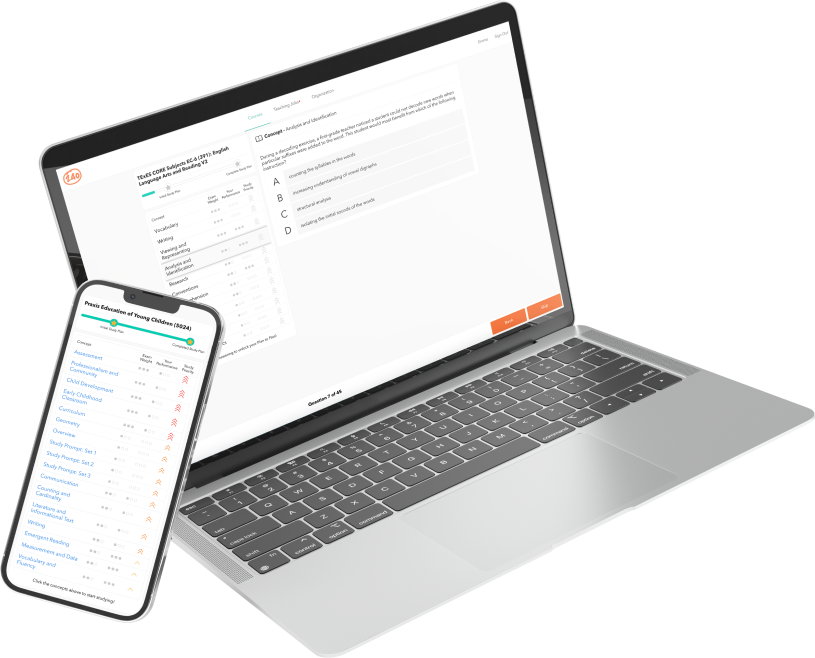
The TExES Physical Science 6-12 (237) exam covers four domains of learning. The exam aims to determine the readiness of Texas educators to teach physical sciences across the 6-12 levels.

Format: 

Test material includes 100 questions taken from topics across scientific inquiry, physics, chemistry, and science learning. The total test time is five hours, including 15 minutes for a computer-administered test (CAT) tutorial.

Cost: 

$116

Scoring: 

Test takers can score between 100 and 300 points and need a minimum score of 240 to pass. Test scores are released online 3-4 weeks after the test date.

Pass rate: 

In 2016-2017, the reported pass rate was 44%, with an average score of 229.07.

Study time: 

The Texas Education Agency recommends making a study plan and starting the study process early. Study plans help test takers know what to expect, identify useful prep materials, and implement a strategy for success. Sticking to the study schedule with regular study sessions and practicing different kinds of sample questions is the best way for students to prepare for the exam.

What test takers wish they’d known: 

• Points are awarded for correct answers but not deducted for wrong answers.
• Reference materials provided by the test site include a periodic table, definitions and physical constants, and an on-screen scientific calculator.
• Reference materials can be reviewed before the test date at https://www.tx.nesinc.com/
• Exam appointments can be canceled and rescheduled through your online account up to 48 hours before the test.
• You should plan to arrive at least 20 minutes before your scheduled test time. Late arrivals may not be allowed to take the test. Refunds will NOT be provided.
• Two valid forms of photo id are required to sign in at the testing center.
• Visitors, including relatives, children, and friends, are NOT allowed to accompany the test taker to the test site.
• Personal items, including phones, watches, purses, hats, pens, and pencils, are NOT allowed in the testing room.
• Food and drinks are NOT allowed in the testing room.
• Required security steps include lifting hair, pushing up sleeves, turning out pockets, and patting yourself down.
• Test takers are monitored by video for the duration of the exam.
• You can request a break by raising your hand. Time will not stop for an unscheduled break.
• Exam retakes are allowed after 45 days. Only five total attempts are allowed.

Information and screenshots obtained from the TExES and NES website.

TExES Physical Science 6-12 Domain I: Scientific Inquiry and Processes

Overview

Domain I of the TExES Physical Science 6-12 Test includes about 14 multiple-choice questions. There are three competencies within this domain.

Let’s explore some specific concepts within this domain.

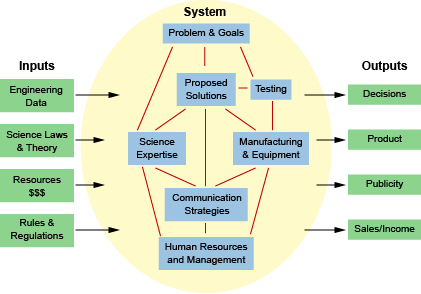
Systems Model

A systems model is a method for organizing different parts of a system. A system includes all the component parts of a single process or idea. For example, a forest ecosystem includes a network of all the living organisms, nonliving structures, and environmental processes in the forest.

Another example of a system could be an experiment in which objects of different shapes are dropped from a height to measure air resistance. The general diagram below can be applied to the specific components of this system.

The system model for this experiment may include:

• inputs – physical laws, gravitational constants, rules regarding the experiment site, and data from pilot studies
• system – the problem, aim, hypothesis, equipment, experimental design, and research staff
• outputs – any future decisions, policies, or innovations that come from the experiment
• feedback loops – outputs that go back into the system to improve the model

Stay Safe in Labs

Safety should always be a primary objective in a laboratory environment. Lab safety rules include the following:

• Do NOT return chemicals to their container. Dispose of excess to avoid cross-contamination.
• ALWAYS dispose of liquid waste in properly labeled containers.
• ALWAYS wear personal protective equipment, including goggles, gloves, lab coat, long pants, and closed-toe shoes in the lab.
• ALWAYS wash hands when entering and leaving the lab and before touching any personal items in the lab (phone, keys, etc.).
• NEVER open a chemical container towards the face. Direct open containers towards the back of a fume hood.
• NEVER use chipped glassware. Dispose of broken glassware in the appropriate waste container.
• NEVER eat, drink, or store food or drinks in the lab.
• NEVER breathe in chemicals. Assess odors by gently wafting the air towards the face.
• NEVER taste chemicals.
• ALWAYS keep electrical outlets dry and clear from clutter. Do NOT overload electrical outlets.
• ALWAYS notify the teacher immediately in the case of chemical spill, fire, or injury.
• Regularly review the location of emergency exits and safety equipment (eyewash, shower, fire blanket, fire extinguisher, etc.).
• Regularly test that emergency safety equipment is available and in working condition.

Scientific Inquiry

Scientific inquiry refers to established systems and methodologies for learning through observation and experimentation. Important components of scientific inquiry include testing a hypothesis, analyzing data, and formulating conclusions based on the data. Scientific inquiry strives to be objective. This differs from nonscientific inquiry, which may include subjectivity in the form of personal experiences, deference to authority figures, and the influence of previous bias.

That is some information about TExES Physical Science 6-12 Domain I.

TExES Physical Science 6-12 Domain II: Physics

Overview

Domain II of the TExES Physical Science 6-12 Test has about 36 multiple-choice questions. There are eight competencies within this domain.

Let’s explore some specific concepts within this domain.

Bernoulli’s Principle

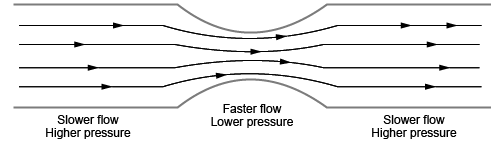
Bernoulli’s principle relates the velocity, or speed, of a fluid to pressure. In fluid dynamics, this means that the speed of a horizontal flow is inversely proportional to the pressure on the fluid. For example, water flowing through a horizontal pipe will flow faster in areas where the pipe has a smaller diameter compared to areas where the pipe has a larger diameter.

Bernoulli’s principle can also be applied to airflow in a phenomenon called airfoil. The wings of an airplane are designed to be curved on the top and flat on the bottom. This forces the air going over the top of the wing to flow faster than air flowing under the wing. The faster-flowing air is at a lower pressure, which creates an upward lift force perpendicular to the flow.

Drawing Free Body Diagrams (FBDs)

Free body diagrams (FBD) are a visual representation of all the forces acting on an object. FBDs are used to solve mechanics problems in physics.

The following FBD shows the forces associated with a sled that is pushed to the right along a horizontal surface.

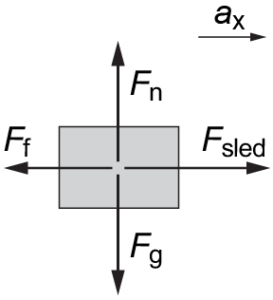
The basic steps to drawing this FBD are listed below.

1. Draw a rectangle to represent the sled as a rigid, solid body.
2. Add the direction of acceleration (a_x).
3. Add the force of gravity (F_g) vector straight down.
4. Add the normal force (F_n) vector perpendicular to the surface that the object is on.
   • On a horizontal surface, F_n is opposite to F_g.
5. Add applied forces (F_sled) vector in the direction of a_x.
6. Add the frictional force (F_f) vector in the opposite direction to F_sled.
   • The F_f vector is shorter than F_sled to denote a smaller magnitude.

The Electrostatic Force

Electrostatic force refers to the attraction and repulsion between charged objects. Opposite charges have an attractive force and like charges have a repellent force.

Use Coulomb’s law to calculate the force between two charged particles:

F = K q₁q₂/r²

where

K (Coulomb’s constant) = 1/4????ε₀ ≈ 9 x 10⁹ N ᐧm²/C²

q₁ = magnitude of the first point charge in coulombs
q₂ = magnitude of the second point charge in coulombs

r = distance between the two charges in meters

Example 1:

Find the distance needed for two oppositely charged point charges of 10 coulombs to have an attractive force equal to 1000 N.

1. 1. Solve the Coulomb’s equation for distance: F = K q₁q₂/r²
      r² = Kq₁q₂/F ⇒ r = √(Kq₁q₂/F)
   2. Since the charges are identical q₁ = q₂r = √(Kq²/F)
   3. Substitute in known values and calculate r:r = √(9 x 10⁹ N ᐧm²/C²(10 C)²/1000 N)

= 30000 m

The Electromagnetic Spectrum

The electromagnetic spectrum describes a range of electromagnetic radiation with different wavelengths. Electromagnetic radiation comes from the movement of light particles called photons, traveling in waves with specific frequencies. High energy photons have short wavelengths and high frequencies. Low energy photons have long wavelengths and low frequencies.

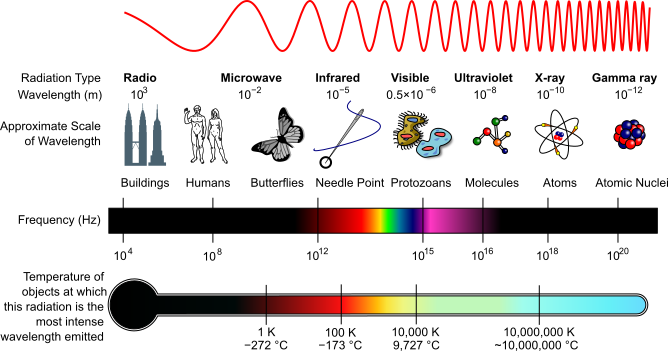
Different sections of the electromagnetic spectrum are summarized below.

High energy waves

• Wavelength from 1pm to 100 nm
• Frequency from 100 EHz to 30 PHz
• Ionizing radiation including gamma rays, X-rays, ultraviolet rays

Visible light waves

• approximate wavelength by color
  • red 700-635 nm
  • orange 635-590 nm
  • yellow 590-560 nm
  • green 560-520 nm
  • cyan 520-490 nm
  • blue 490-450 nm
  • violet 450-400nm
• frequency from 430-750 THz

Lower energy waves

• wavelength from 10 μm to 100,000 km
• frequency from 30 THz to 3 Hz
• includes infrared waves, microwaves, and radio waves

Types of Magnetism

Magnetism is a property of matter that comes from the orbital movements of electrons. Some elements experience strong magnetic fields, some can be induced to form a magnet, and some elements are not affected by magnetic fields.

Diamagnetism

• repelled by magnetic fields
• diamagnetic elements include H, Be, nonmetals, halogens, noble gases

Paramagnetism

• magnetic when exposed to a magnetic field
• weakly attracted to magnetic fields
• magnetic elements include alkali and alkaline earth metals, transition metals, O, Al, Sn

Ferromagnetism

• always magnetic
• strongly attracted to magnetic fields
• ferromagnetic elements include iron, nickel, cobalt

Ohm’s Law

Ohm’s law is used to describe how current flows through a conductor. Ohm’s law states that the current (I) between two points with some resistance (R) is proportional to the voltage differential (V).

I = V/R

Example:

What is the resistance of a conductor with 1.25 Amp of current and a 4.1 V battery?

1. Set up the equation and solve for R:I = V/R
   ⇒ R = V/I
2. Substitute values:I = 1.25
   V = 4.1 V

R = 4.1 / 1.25
= 3.28 Ω resistance

At a constant resistance, an increase in the applied voltage increases the current through the conductor. Likewise, at a constant voltage, an increase in the resistance decreases the flow of current.

Kinetic Molecular Theory – Arrhenius Equation

Kinetic molecular theory describes the behavior of particles. Applied to gases, kinetic molecular theory makes the following assumptions:

1. Particles are spherical objects with no mass and negligible volume relative to the volume of the container.
2. Particles move in random straight paths until they collide with the side of the container or other particles.
3. Particles are inert and do not attract or repel other particles.
4. Collisions between particles are completely elastic. There is no loss of energy.
5. The average kinetic energy of particles in a container depends only on temperature.

The Arrhenius equation applies kinetic molecular theory to chemical reactions. The Arrhenius
equation is stated as

k = Ae^-Ea/RT

where

k = reaction rate constant
A = pre-exponential factor constant
E_a = activation energy for the reaction (J mol^-1)
R = universal gas constant, 8.314 J mol^-1 K^-1
T = temperature in K

The important relationship here is in the exponent -E_a/RT. RT is equal to the average kinetic energy, so -Ea/RT is a ratio of activation energy to average kinetic energy.

A small ratio, in which the activation energy is low and temperature is high, leads to larger rate constants and faster reactions. Conversely, a large ratio, in which activation energy is high and temperature is low, leads to smaller rate constants and slower reactions. A general rule is that a 10 K rise in temperature corresponds to a doubling of reaction rate.

Example

Find the activation energy (E_a) for a chemical reaction with a rate constant (k) of 18 M^-1s^-1 and a pre-exponential factor (A) of 20 M^-1s^-1 at

• • 279 K
  • 299 K

1. Write out the Arrhenius equation and solve for activation energy E_a:
   • k = Ae^-Ea/RT
   • ⇒ ln(k) – ln(A) = -E_a/RT
   • ⇒ E_a = -RTln(k/A)
2. Substitute in values and solve:
   • T = 279 K, A = 20 M^-1s^-1 , k = 18 M^-1s^-1, R = 8.314 J mol^-1 K^-1
     ;
     • E_a = -RTln(k/A)
     • = – 8.31(279)ln(18/20)
     • = 244.277 J/mol
   • T = 299 K, A = 20 M^-1s^-1 , k = 18 M^-1s^-1, R = 8.314 J mol^-1 K^-1
     • E_a = -RTln(k/A)
     • = – 8.31(299)ln(18/20)
     • = 261.788 J/mol

Rate constant increases as the ratio of activation energy to temperature decreases. To compensate for holding a steady rate constant at a higher temperature, the activation energy must increase.

Properties of Waves

Waves describe a transfer of energy between two objects. Waves differ from particles of matter in that they do not have mass, only energy. Examples of waves in nature include waves through water, seismic waves through the earth, and sound and light waves through air.

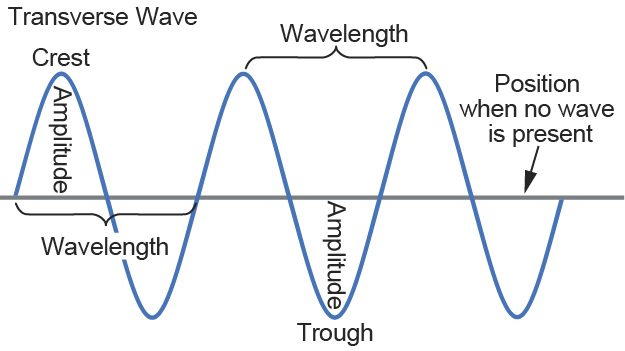
Universal properties of waves include the following:

• Amplitude is the height of the wave, or the distance from the origin to the trough or crest. Amplitude is measured in meters (m) and corresponds to the maximum displacement from the vibration of a wave.

• Wavelength (λ) is the distance between crests or troughs, and it is measured in meters. Wavelength is inversely related to frequency, so a longer wavelength means that there are fewer wave cycles per second.

• Period is the time it takes for the wave to complete one cycle, or the time it takes for the wave to travel one wavelength. Period is inversely related to frequency and directly related to wavelength such that

• • Period = 1/f, and
  • Period = λ/v
• Frequency (f) measures the number of wave cycles that pass through a fixed point in 1 second. Frequency is measured in hertz (Hz), and it is inversely related to period and wavelength such that

• • f = 1/period, and
  • f = speed of light/λ.
• Velocity measures the speed of the wave in meters per second and can be calculated by
  • v = λ · f

That is some information about TExES Physical Science 6-12: Domain II: Physics.

TExES Physical Science 6-12 Domain III: Chemistry

Overview

Domain III of the TExES Physical Science 6-12 Test has about 41 multiple-choice questions. There are nine competencies within this domain.

Let’s explore some specific concepts within this domain.

Chemical Equilibrium

When a chemical reaction reaches equilibrium, the forward reaction rate equals the reverse reaction rate. Chemical equilibrium is a state of dynamic equilibrium with no NET production. This means that the reaction is still happening, but the products and reactants are being consumed at an equal rate.

While the forward and reverse reaction rates are equal at chemical equilibrium, the concentrations of different reagents can differ. Whether equilibrium favors products or reactants can be determined with the equilibrium constant (K) expression.

For the chemical reaction

aA + bB ⇋ cC + dD

the equilibrium constant (K) expression is the ratio of the concentration of products to reactants with each species raised to the power of its coefficient.

K = [C]^c[D]^d/[A]^a[B]^b

If K > 1, then there are more products than reactants at equilibrium.
If K < 1, then there are more reactants than products at equilibrium.
If K = 1, then there are equal concentrations of products and reactants at equilibrium.

Acids, Bases, and Salts

Water is sometimes called the universal solvent because it is able to dissolve a large range of chemical compounds. Acids, bases, and salts are all generally soluble in water. The specific characteristics of acids, bases, and salts are described below.

Acids lower the pH of a solution and bases raise the pH of a solution. There are three systems for defining acids and bases. While many common acids or bases will fit all three definitions, there are some exceptions.

1. Arrhenius acids and bases are compounds that produce H⁺/OH^– ions in solution.

• Example:
  • Acid: aqueous solution of hydrochloric acid (HCl) produces H⁺
    HCl (aq) → H⁺ (aq) + Cl^– (aq)
  • Base: aqueous solution of sodium hydroxide (NaOH) produces OH^–
    NaOH (aq) → OH^– (aq) + Na⁺ (aq)
• Exception:
  • Acid: any acidic compound not in the general form of HA or in a solution with water such as CO₂ (g) and HCl (g)
  • Base: any basic compound not in the general form of BOH or in a solution with water such as NH₃ (g).

2. Brønsted-Lowry acids release or donate a hydrogen ion (H⁺), and Brønsted-Lowry bases accept H⁺. This theory expands on Arrhenius acids by referring to the action of H⁺ rather than H⁺ and OH^–.

• Example:
  • Acid: hydroiodic acid donates H⁺ to water, forming hydronium (H₃O⁺)
    HI (aq) + H₂O (l) → H₃O+ (aq) + I^– (aq)
  • Base: water accepts H⁺ from hydroiodic acid, forming hydronium (H₃O⁺)
• Exception:
  • Acid: aluminum (III) chloride (AlCl₃) is not considered a Brønsted-Lowry acid because it doesn’t contain H⁺ to donate, but it hydrolyzes in water to form hydrochloric acid, lowering pH.

3. Lewis acids accept a shared electron pair, forming a covalent bond. Lewis bases donate a shared electron pair. This theory expands on Brønsted-Lowry by referring only to the action of electrons rather than H⁺ in solution.

• Example:
  • Acid: all Brønsted-Lowry acids + acid compounds without H⁺ such as AlCl₃, BBr₃, BF₃
  • Base: all Brønsted-Lowry bases

Strong acids and bases are compounds that dissociate completely in water. Weak acids and bases only partially dissociate in water.

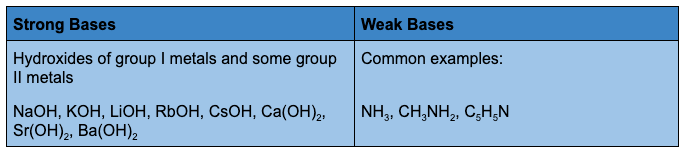
Salts are ionic compounds produced by chemical reactions between acids and bases. Salts are composed of a positively charged cation and a negatively charged anion connected by an ionic bond. The neutralization of sodium hydroxide with hydrochloric acid forms sodium ions (Na⁺) and chloride ions (Cl^–) that form solid NaCl when dried.

NaOH (aq) + HCl (aq) → H₂O (l) + Na⁺ (aq) + Cl^– (aq)

Solid salts have a crystalline lattice structure. In solutions, salts act as electrolytes, conferring the ability of a solution to conduct an electric charge. Salts can also have acid or base activity.

• Neutral salts are the product of a strong acid reacting with a strong base and do not affect the pH when dissolved in a solution. Examples include NaCl, KI, and MgSO₄.
• Acidic salts are the product of a strong acid reacting with a weak base and lower the pH when dissolved in a solution. Examples include NaHSO₄, MgCl₂, and NH₄Cl.
• Basic or alkali salts are the product of a strong base reacting with a weak acid and raises the pH when dissolved in a solution. Examples include Na₂CO₃, NaHCO₃, and K₂S.

Nuclear Energy: Fission vs. Fusion

Nuclear reactions involve the transfer of energy between atomic nuclei.

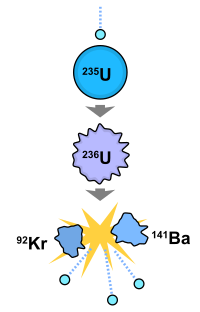
In nuclear fission, an atomic nucleus is split into lighter nuclei and emission products including neutrons and high-energy waves of gamma radiation. The energy released by nuclear fission is an energy source that can be used to produce electricity.

In the image below, an extra neutron joins uranium-235, forming uranium-236. The heavier atom is in an unstable, excited state, which relaxes through nuclear fission. Uranium-236 splits into the lighter elements krypton-92 and barium-141. The reaction also releases three extra neutrons and high-energy gamma rays.

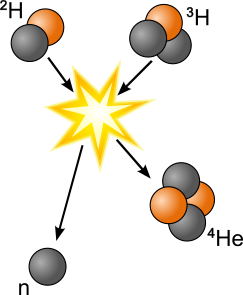
In nuclear fusion the nuclei of small elements combine to form heavier atoms, often releasing neutrons. Nuclear fusion reactions can be exothermic or endothermic. Solar energy is a product of the exothermic nuclear fusion of hydrogen atoms in the star’s core.

Fusion products that are lighter than iron were most likely formed in an exothermic reaction; the products are lower-energy than the reactants and energy is transferred to the environment as heat.

Products that are heavier than iron form in an endothermic reaction; the products are higher-energy than the reactants and the extra energy is transferred from the environment as heat.

In the image below, the fusion of deuterium (1 neutron + 1 proton) and tritium (2 neutrons + 1 proton) forms helium (2 neutrons + 2 protons). This is an exothermic reaction, so the extra neutron and 17.59 MeV of energy are transferred to the environment.

Balancing Chemical Reactions

The law of conservation of mass states that mass cannot be created or destroyed in a chemical reaction. This means that while the arrangement of atoms between the reactants and products may change, the total number of atoms must stay the same. For example, if the reactants have two atoms of oxygen, then the products must also have two atoms of oxygen.

A chemical reaction that follows the law of conservation of mass is balanced. Refer to the following tips for balancing chemical equations:

• Multiply by subscripts to get the total number of atoms.
• Add coefficients to balance chemical equations.
• Always recheck after adding coefficients.

Example 1: Use coefficients to balance the chemical equation:

H₂ + F₂ → HF

1. Find the total number of atoms by multiplying each atom by its subscript:

Reactants: 2 atoms of H and 2 atoms of F
Products: 1 atom of H and 1 atom of F

2. Add a coefficient to HF in the products:

H₂ + F₂ → 2HF

3. Check that the new equation is balanced:

Reactants: 2 atoms of H and 2 atoms of F
Products: 2 atom of H and 2 atom of F

• For more complicated reactions, balance elements other than O and H first. Carbon, metals, and other larger atoms are usually the central atoms of molecules and appear less frequently than O and H.

Example 2: Use coefficients to balance the equation for the combustion of propanol.

C₃H₇OH (l) + O₂ (g) → CO₂ (g) + H₂O (g)

1. Find the total number of atoms by multiplying each atom by its subscript:

Reactants: 3 atoms of C, 8 atoms of H, 3 atoms of O
Products: 1 atom of C, 2 atoms of H, 3 atoms of O

2. Start by balancing C with a coefficient of 3 on CO₂, and recheck the total number of atoms.

C₃H₇OH (l) + O₂ (g) → 3CO₂ (g) + H₂O (g)

Reactants: 3 atoms of C, 8 atoms of H, 3 atoms of O
Products: 3 atom of C, 2 atoms of H, 7 atoms of O

Adding a coefficient to CO₂ increases the total number of O atoms in the products.

3. Balance H by adding a coefficient of 4 to H₂O and recheck the total number of atoms.

C₃H₇OH (l) + O₂ (g) → 3CO₂ (g) + 4H₂O (g)

Reactants: 3 atoms of C, 8 atoms of H, 3 atoms of O
Products: 3 atom of C, 8 atoms of H, 10 atoms of O

Adding a coefficient to H₂O increases the total number of O atoms in the products.

4. Balance O by adding a coefficient to O₂, and recheck the total number of atoms. It’s okay to have a fraction as a coefficient.

C₃H₇OH (l) + 9/2O₂ (g) → 3CO₂ (g) + 4H₂O (g)

Reactants: 3 atoms of C, 8 atoms of H, 10 atoms of O
Products: 3 atom of C, 8 atoms of H, 10 atoms of O

• Divide out spectator ions in aqueous reactions to find the balanced net ionic equation.

Example 3: Balance the double displacement reaction and write the net ionic equation.

KBr (aq) + Pb(NO₃)₂ (aq) → K(NO₃) (aq) + PbBr₂ (s)

1. Balance polyatomic ions by adding coefficients:

Reactants: 1 ion of K⁺, 1 ion of Br^– , 1 ion of Pb²⁺, 2 ions of NO₃^–
Products: 1 ion of K, 2 ions of Br^– , 1 ion of Pb²⁺, 1 ion of NO₃

2KBr (aq) + Pb(NO₃)₂ (aq) → 2K(NO₃) (aq) + PbBr₂ (s)

Because lead(II) has a charge of +2, it bonds with two molecules of nitrate (NO₃^–) in the reactants and two molecules of bromide (Br^–) in the products. This equation is balanced by adding coefficients to the compounds that do not contain Pb²⁺.

2. Check that the total ions are balanced:

Reactants: 2 ion of K⁺, 2 ion of Br^– , 1 ion of Pb2+, 2 ions of NO₃^–
Products: 2 ion of K⁺, 2 ions of Br^– , 1 ion of Pb²⁺, 2 ion of NO₃

3. Break up aqueous species, and write the full ionic equation:

2K⁺ (aq) + 2Br^– (aq) + Pb²⁺ (aq) + 2NO₃^– (aq) → 2K⁺ (aq) + 2NO₃^– (aq) + PbBr₂ (s)

4. Divide out spectator ions, and write the net ionic equation

2K⁺ (aq) + 2Br^– (aq) + Pb²⁺ (aq) + 2NO₃^– (aq) → 2K⁺ (aq) + 2NO₃^– (aq) + PbBr₂ (s)

⇒ 2Br^– (aq) + Pb²⁺ (aq) → PbBr₂ (s)

Balancing Chemical Reactions – Redox

Oxidation reduction (redox) reactions involve a transfer of electrons between the reactants to form the products. Chemicals that gain electrons are reduced, and chemicals that lose electrons are oxidized.

Example 1:

Balance the following equation, and Identify which chemical is oxidized and which is reduced:

H₂ (g) + Cl₂ (g) → HCl (g)

1. Balance by adding a coefficient to the products:

H₂ (g) + Cl₂ (g) → 2 HCl (g)

2. Split the full reaction into half reactions for each reactant:

H₂ → 2H⁺ ; the charge on H is increasing from 0 to +1 ⇒ oxidation
Cl₂ → 2Cl^– ; the charge on Cl is increasing from 0 to -1 ⇒ reduction

3. Balance the half reactions by adding electrons to the more positive side:

Oxidation: H₂ → 2H⁺ + 2e^–
Reduction: Cl₂ + 2e^– → 2Cl^–

Example 2:

Balance the following redox equation between copper and tin:

Sn (s) + Cu²⁺ (aq) → Cu (s) + Sn⁴⁺ (g)

1. Determine the half reactions for oxidation and reduction:

Oxidation: Sn → Sn⁴⁺
Reduction: Cu²⁺ → Cu

2. Balance the half reactions by adding electrons to the more positive side:

Oxidation: Sn → Sn⁴⁺ + 4e^–
Reduction: Cu²⁺ + 2e^– → Cu

3. Multiply both half reactions to achieve the least common multiple of electrons:

Oxidation: (Sn → Sn⁴⁺ + 4e^–) x 1
Reduction: (Cu²⁺ + 2e^– → Cu ) x 2

In this case, the least common multiple for electrons is 4, so the reduction half reaction gets a coefficient of 2 applied to each reagent.

4. Combine the half reactions, canceling out the electrons from each side:

Oxidation: Sn → Sn⁴⁺ + 4e^–
Reduction: 2Cu²⁺ + 4e^– → 2Cu

Sn (s) + 2Cu²⁺ (aq) + 4e^– → 2Cu (s) + Sn⁴⁺ (aq) + 4e^–

⇒ Sn (s) + 2Cu²⁺ (aq) → 2Cu (s) + Sn⁴⁺ (aq)

Example 3:

Balance the following redox reaction in an acidic solution:

Ag (s) + Fe³⁺ (aq) → Ag₂O (aq) + Fe (s)

1. Determine the half reactions for oxidation and reduction:

Oxidation: Ag → Ag₂O
Reduction: Fe³⁺ → Fe

2. Balance atoms other than O and H. Then add water (H₂O) molecules to balance O, and hydrogen ions (H⁺) to balance H:

Oxidation: 2Ag + H₂O → Ag₂O + 2H⁺
Reduction: Fe³⁺ → Fe

3. Balance the charge by adding electrons to the more positive side:

Oxidation: 2Ag + H₂O → Ag₂O + 2H⁺ + 2e^–
Reduction: Fe³⁺ + 3e^– → Fe

4. Multiply both half reactions to achieve the least common multiple of electrons:

Oxidation: (2Ag + H₂O → Ag₂O + 2H⁺ + 2e^–) x 3
Reduction: (Fe³⁺ + 3e^– → Fe) x 2

5. Combine the half reactions, canceling out the electrons from each side:

Oxidation: 6Ag + 3H₂O → 3Ag₂O + 6H⁺ + 6e^–
Reduction: 2Fe³⁺ + 6e^– → 2Fe
6Ag (s) + 3H₂O (l) + 2Fe³⁺ (aq) + 6e^– → 2Fe (s) + 3Ag₂O (aq) + 6H⁺ (aq) + 6e^–
⇒ 6Ag (s) + 3H₂O (l) + 2Fe³⁺ (aq) → 2Fe (s) + 3Ag₂O (aq) + 6H⁺ (aq)

Nuclear Chemistry – Half-Life Calculations

Atomic nuclei change over time through radioactive decay processes. The rate of decay is described in terms of half-life, which is the time it takes for half the mass of a given sample to decay. Half-life is specific to the identity of the material and independent of factors such as temperature and concentration.

For example, 10 g of a radioisotope with a half-life of 2 years will have 5 g remaining after two years, 2.5 g remaining after 4 years, 1.25 g remaining after 6 years, and so on.

Where n is the number of half-lives, the final mass (N₁) is given by

(1) N₁ = N₀(½)ⁿ

If the half-life of a material is unknown then the following equation

(2) N_t = N₀(½)^t/t1/2

can be used to solve for half-life t_1/2

where

N_t ⇒ final mass
N₀ ⇒ initial mass
t ⇒ time elapsed
t_1/2 ⇒ half life

The full equation (2) above can be simplified to the equation for exponential decay:

N_t = N₀e^-λt

where

λ ⇒ decay constant, or ln(2)/t_1/2

Example:

Find the half-life of a radioisotope that decays from 25.2 g to 0.3 g over 100 years rounded to
the nearest year.

1. Write the half-life equation in exponential decay form and solve for the decay constant (λ):

N_t = N₀e^-λt
⇒ N_t/N₀ = e^-λt
⇒ ln(N_t/N₀) = -λt
⇒ λ = ln(N_t/N₀)/ -t

2. Substitute in values for final mass (N_t), initial mass (N₀), and time (t):

λ = ln(N_t/N₀)/ -t

λ = ln(0.3/25.2)/ -100
= 0.044

3. Use the relationship between the decay constant and t_1/2 to find the half-life:

λ =ln(2)/t_1/2
⇒ t_1/2 = ln(2)/λ

t_1/2 = ln(2)/(0.044)
= 15.75
≈ 16 years

This means that there have been 6.25 half-lives in 100 years. It is possible to check the answer by substituting the number of half-lives that have elapsed into equation (1).

N₁ = N₀(½)ⁿ

N₁ = 25.2(½)^6.25
= 0.33 g

which is about equal to the expected final amount, 0.3 g.

Endothermic vs. Exothermic

In reactions where the products are lower-energy than the reactants, there is a net transfer of energy to the environment from the reaction. Exothermic processes release heat energy, which raises the temperature of the surroundings.

Combustion reactions are exothermic. For example, a log of wood burns in the presence of oxygen, producing carbon dioxide, water vapor, and heat. The chemical bonds in the wood store energy, and as these bonds are broken during combustion the excess energy is released as heat.

In reactions where the products are higher-energy than the reactants, there is a net transfer of energy from the environment to the reaction. Endothermic processes absorb heat energy, which lowers the temperature of the surroundings.

Evaporation of liquid water to water vapor is endothermic. Hydrogen bonds between water molecules store energy. Breaking these bonds requires an initial input of heat energy, which dissipates as the water enters the vapor phase. This phenomenon is also called evaporative cooling.

Types of Bonds

Chemical bonds between adjacent atoms form molecules. These intramolecular (“within molecule”) bonds are stronger than intermolecular (“between molecule”) bonds that form molecular associations.

The three main types of chemical bonds are covalent bonds, ionic bonds, and metallic bonds. The following table summarizes the main properties of each type of intramolecular bond.

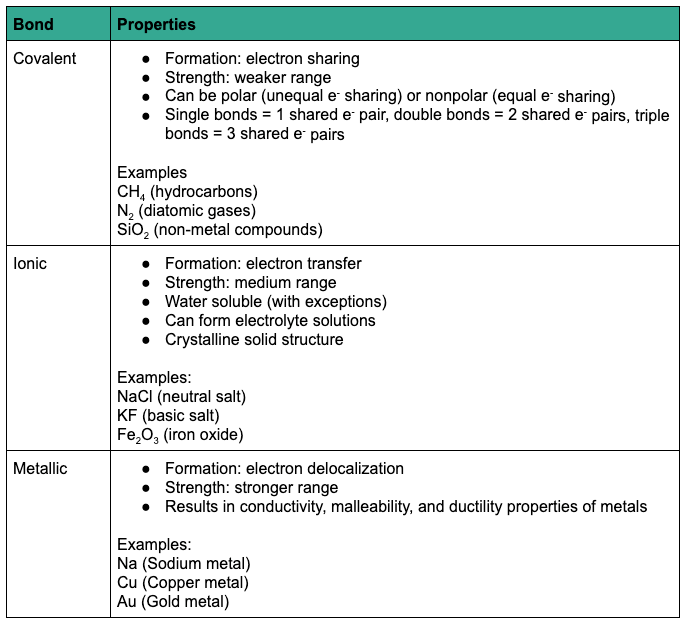
And that is some information about TExES Physical Science 6-12 Domain III: Chemistry.

TExES Physical Science 6-12 Domain IV: Science Learning, Instruction, and Assessment

Overview

Assessment Validity

Educators use assessments to report student achievement, monitor progress, and standardize learning outcomes. Assessments can be formative or summative. Formative assessments refer to ongoing testing in the form of benchmarks or quizzes, and summative assessments test knowledge and skills gained during a unit, semester, etc.

The properties that determine effective assessment practices are described below.

Assessments should have the following attributes:

1. Congruency

Assessment congruency means that both the instructional material and assessments are designed to support the learning objectives.

For example, a learning objective to explain the use of a catalyst in a chemical reaction can be supported by a lab activity and an assessment question on the activity setup.

2. Reliability

Reliability means that the scores of a particular assessment can be trusted to accurately represent student knowledge. A reliable assessment results in consistent scores when taken multiple times.

For example, a class that takes a mechanics assessment on Tuesday should receive a similar mean score after testing on the same material on Friday. Additionally, the students should miss questions at a constant rate throughout the entire assessment rather than missing, say, an overwhelming majority of questions from the last page.

3. Validity

A valid assessment results in higher scores for students who have learned the instructional material and achieved learning objectives. Assessment validity refers to how closely related the test is to the instructional material.

For example, after a unit on electric circuits, students should do well on assessment questions about Ohm’s law and poorly on assessment questions about nuclear reactions.

4. Absence of bias

Absence of bias is related to assessment validity. Bias in assessments can offend students, distracting them from answering correctly, or exclude students who lack experience on a concept because of their socioeconomic background.

For example, a question on Galileo Galilei that requires prior knowledge of the architecture of the Tower of Pisa can exclude students who don’t know about European culture and/or lack the resources to travel internationally. Additionally, an assessment that uses masculine pronouns to refer to all scientists may be frustrating and distracting to feminine/nonbinary students.

5. Clarity of language

Clarity of language is related to assessment validity. If students are confused by the language, then an assessment cannot accurately measure how well the instructional material was learned.

For example: A question on kinetic molecular theory that uses only the acronym KMT may cause students who have achieved learning objectives on kinetic molecular theory to miss the question.

6. Appropriate levels

Using the appropriate level for reading and content are related to validity. If students are confused by the language, then an assessment cannot accurately measure how well the instructional material was learned.

For example, a 7th-grade-level question on chemical bonds that is written to the reading level of a university English literature class may confuse students who have achieved learning objectives in chemistry.

ELL Students

Students who are English language learners (ELL) may need extra resources or accommodations to learn the instructional material. However, many of the following practices can benefit all students.

• Provide a list of key terms for each unit.
• Include diagrams, graphic organizers, charts, graphs, and visual aids to help students see the information in different ways.
• Turn on closed captioning and pause frequently in video clips.
• Incorporate hands-on, collaborative, and group activities to encourage communication and teamwork.
• Provide study guides, syllabi with assignment dates, and outlines of coursework.
• Give clear and unambiguous instructions.
• Practice consistent routines and expectations in the classroom.
• Define new vocabulary words with pictures.
• Explain the root meaning of new scientific words. Many Greek and Latin roots are shared between different languages.
• Construct a word wall with pictures that students can reference for commonly used terms.
• Provide sentence stems to help students phrase their answers; for example, “The forces acting on an object at rest are …”

And that’s some basic information about the TExES Physical Science 6-12 test.

Take the TExES Physical Science 6-12 (237) Practice Test