TExES Math 7-12 Key Concepts to Know
The exam has six domains:
- Number Concepts (14%)
- Patterns and Algebra (33%)
- Geometry and Measurement (19%)
- Probability and Statistics (14%)
- Mathematical Processes and Perspectives (10%)
- Mathematics Learning, Instruction, and Assessment (10%)
Number Concepts

The Number Concepts domain has about 14 questions. These questions account for 14% of the entire exam.
This domain can be neatly divided into 3 competencies:
- The Real Number System
- The Complex Number System
- Number Theory Concepts and Principles
Let’s talk about a concept that you will more than likely see on the test.
Subsets of the Real Number System

Patterns and Algebra




The Patterns and Algebra domain has about 33 questions. These questions account for 33% of the entire exam.
This domain can be neatly divided into 7 competencies:
- Patterns
- Functions, Relations, and Their Graphs
- Linear and Quadratic Functions
- Polynomial, Rational, Radical, Absolute Value, and Piecewise Functions
- Exponential and Logarithmic Functions
- Trigonometric and Circular Functions
- Calculus
Here are some concepts you will see on the test.
Compound Interest
To calculate continuous compound interest, use the formula below:After t years, the balance A in the account with principal P and annual interest rate r is given by the equation:
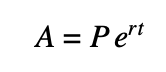
The principal P is the amount in the account at the beginning of the period. The rate r should be written as a decimal.For example, find the accumulated value of an investment of $4,000 for 8 years at an interest rate of 3.4% compounded continuously.

Finding Inverse Functions

Solving Quadratic Equations
Quadratic equations are equations where the variable has degree 2.
Let’s solve the quadratic equation:5x²+ x = 2
Some quadratic equations can be solved by factoring; however, this equation can only be solved algebraically by using the quadratic formula or by graphing. We will solve using the quadratic formula.
To use this method, first put the equation into the format
x²+ bx + c = 0. To do this, subtract 2 on both sides of the equation:
5x²+ x – 2 = 0
Now we can see that a = 5, b = 1, and c = -2.
We will plug these coefficients into the quadratic formula:

Geometry and Measurement



The Geometry and Measurement domain has about 19 questions. These questions account for 19% of the entire exam.
This domain can be neatly divided into 4 competencies:
- Measurement
- Euclidean Geometry as Axiomatic Systems
- Euclidean Geometry Results, Uses, and Applications
- Coordinate, Transformational, and Vector Geometry
Take a look at these concepts.
Finding Arc Length
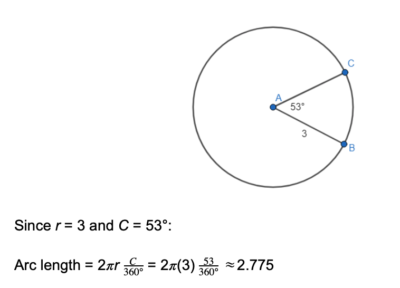
To find the length of an arc of a circle, we need to determine the ratio of the entire circle that it encompasses. The formula for the circumference of a circle is 2???? r , where r is the circumference of the circle; therefore, the length of an arc is a proportion of that.Arc length = 2???? r C360°, where C is the measure of the central angle in degrees.
Look at the circle below. What is the arc length of arc BC ?
Angle Relationships
Angle relationships help us to find missing angles when we are given a diagram, often involving parallel and intersecting lines.
Some important angle relationships are supplementary, complementary, vertical angles, alternate interior angles, and alternate exterior angles.Supplementary angles are angles whose measures add to 180 degrees. If the angles are next to each other, they will form a straight line.Complementary angles are angles whose measures add to 90 degrees. If the angles are next to each other, they will form a right angle.For example, if∡a=48° and∡b=42°, then angle a and angle b are complementary since they sum to 90°.Vertical angles are opposite each other on other sides of two intersecting lines. Vertical angles are always congruent (have equal measure).
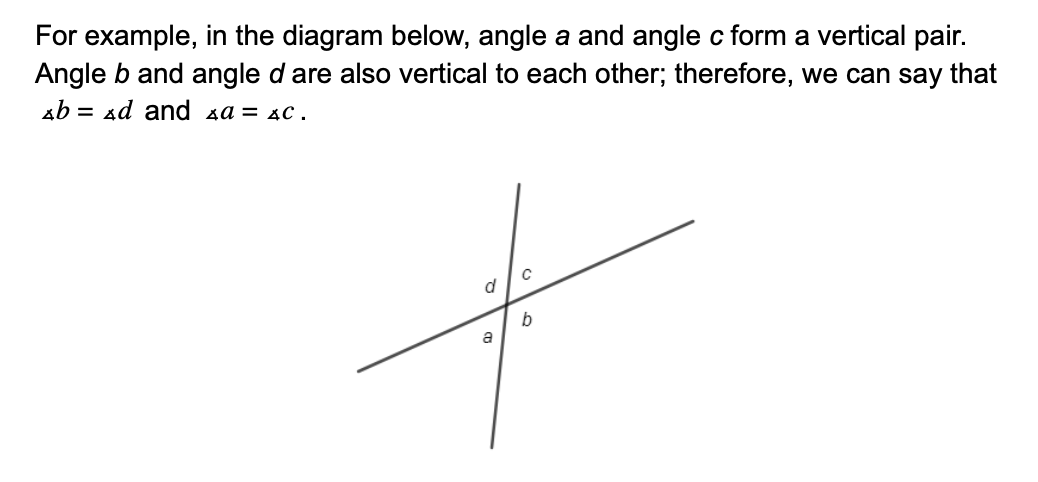
Also, angle a and angle d are supplementary, as are angle a and angle b . Other supplementary pairs are:Angle b and angle c Angle c and angle d A transversal is a line that cuts through at least two other lines.When we have transversals that cut through more than one line, they form alternate angles.Alternate interior anglesare on opposite sides of the transversal but inside the two lines being cut by the transversal.

*NOTE: When the two lines cut by the transversal are parallel to each other, then alternate interior angles are always congruent.
*Likewise, alternate exterior angles are congruent if the two lines cut by a transversal are parallel. These are angles on the outside of the two lines, but opposite each other.
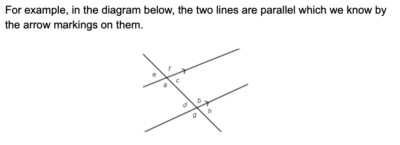
Angle e and angle h are therefore congruent since they are alternate exterior angles. Angle g and angle f are also alternate exterior angles and therefore congruent.
Pythagorean Theorem
The Pythagorean Theorem is used to find the missing side of a right triangle.
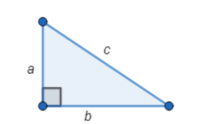
For the right triangle, where a and b are the shorter sides of the triangle, and c is the hypotenuse, then a² + b ² = c ² . Example 1: Suppose we know one side of a right triangle is 10 cm, and the hypotenuse of the triangle is 26 cm. Find the remaining side.
Let a = 10 cm and c = 26 cm. Then we will use the Pythagorean Theorem to find b :a² + b ² = c ² 10² + b ² = 26 ² b² = 26 ² – 10 ² = 576b = √ 576 = 24
Therefore, the remaining side of the triangle is 24 cm.
Example 2: Suppose two people start walking from the same point. After 1 hour, Person A has walked 2.8 miles due north. Person B has walked 3.2 miles due east. Find the distance between them at this time.
Since the two people are walking at right angles to each other, we can apply the Pythagorean Theorem. In this case, the distance between Person A and Person B is the hypotenuse of a right triangle.
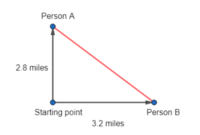
Let a = 2.8 and b = 3.2. Then a² + b² = c ² gives:2.8² +3.2² =c² 18.08 =c² c ≈4.25
Therefore, Person A and Person B are approximately 4.25 miles apart after 1 hour.
Probability and Statistics


The Probability and Statistics domain has about 14 questions. These questions account for 14% of the entire exam.
This domain can be neatly divided into 3 competencies:
- Analyzing and Representing Data
- Probability
- Probability, Sampling, and Statistics
Let’s talk about some concepts that you will more than likely see on the test.
Measures of Central Tendency
Measures of central tendency help us to determine how data is distributed. We will consider several measures of central tendency below.
The mean of a data set is the average value of a data set. This can be found by adding together all of the values and dividing by the total number of values.
The mode of a data set is the value that occurs most frequently in the data set. It is possible to have more than one mode in a data set if several values occur the most.
The median of a data set is the middle value in the set. If there is an even number of data points, there will not be an exact middle. In this case, the median is found by taking the average of the two data points closest to the middle.For example, suppose that the ages for a group of ten students were collected and are listed below:
9, 11, 13, 11, 8, 7, 13, 9, 9, 12
To find the mean of this data set add together all of the values and divide by the total number of values.
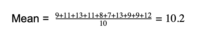
To find the mode and median of a data set, it is helpful to reorder the set from lowest to highest.
7, 8, 9, 9, 9, 11, 11, 12, 13, 13
Now we can see that the mode of the data set is 9, since 9 occurs 3 times, which is more than any other data point.
Since the data set has an even number of values, there are two values in the middle: 9 and 11. To find the median, you must average 9 and 11; therefore, the median of the data set is 10.
An outlier is a data point that is far outside of the normal range of the data set. It is far away from the rest of the data points. For example, suppose that some daily high temperatures in the month of May for a particular area are given below in degrees Fahrenheit:
66, 56, 61, 45, 48, 52, 23, 66, 53, 58, 59
Reordering gives 23, 45, 48, 52, 53, 56, 58, 59, 61, 66, 66
The mean of this data is (66 + 56 + 61 + 45 + 48 + 52 + 23 + 66 + 53 + 58 + 59) /11=53.364
The mode of the data is 66 since this value occurs twice.
The median is 56, since that is the middle value.
However, the temperature of 23 degrees is an outlier, because there is a 22-degree difference between it and any other temperature. Therefore, we can remove this outlier from the data and calculate the mean, mode, and median again to get a better description of the central tendencies of this data set.
45, 48, 52, 53, 56, 58, 59, 61, 66, 66
After the temperature of 23 is discarded, the new mean is 56.4. The mode of the data is still the same in this case since 66 is the only temperature that occurred more than once. The median is now the average of 56 and 58, which is 57 degrees since now there are only ten data points.
Scatterplots
A scatterplot is a graph made up of points in the x – y plane, that show a relationship between two variables x and y.
If the points go up as x increases, then there is a positive correlation between the two variables. For example, there is a positive correlation between the temperature outside and ice cream sales, since as it gets hotter, ice cream sales increase.If the points go down as x increases, then there is a negative correlation between the two variables. For example, there is usually a negative correlation between the number of absences a student has and their grade, since as the absences increase their grade usually decreases.If the points on the scatterplot don’t follow any pattern as x increases, then there is no correlation between the variables. Here are some examples of scatterplots below:
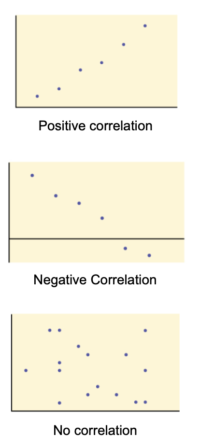
By finding a line of best fit on a scatter plot, predictions can be made about future data points.
For example, a line of best fit is shown for the scatterplot below:
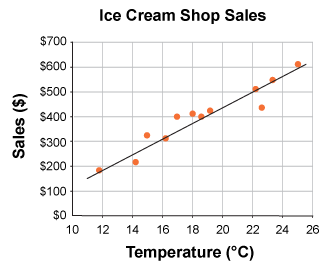
Using this line, we can estimate that when the temperature is 21 degrees Celsius, ice cream sales are around $460.
Mathematical Processes and Perspectives

The Mathematical Processes and Perspectives domain has about 10 questions. These questions account for 10% of the entire exam.
This domain can be neatly divided into 2 competencies:
- Mathematical Reasoning and Problem Solving
- Connections and Communication
Take a look at these concepts that are likely to appear on the test.
Problem Solving Process
The problem-solving process can be broken into steps in various ways, but the basic idea is the same no matter how you state it.
- Re-read the problem. Determine what the question is asking for.
- Determine what information you already know by finding the key details in the problem.
- Choose a strategy to solve the problem.
- Solve the problem.
- Check your answer and make sure that it makes sense in context.
Some problem-solving strategies for mathematics include working backward, looking for a pattern, making an estimate, guess and check, and drawing a picture.
Let’s look at a problem together.
Penny bought some cookies at a bake sale. She ate 3 of them and gave 2 of them to her sister. After dividing the rest equally with her brother, she had 8 cookies remaining. How many cookies did she start with?
This problem can be solved by working backward from the final number of cookies she has at the end of this process. She ends with 8 cookies, which was half of what she had before she shared with her brother. At that point, she had 16 cookies. She gave 2 cookies to her sister. So, she had 18 cookies before doing that. She ate 3 cookies first; therefore, she started with 21 cookies.
Guess and check works well with finding the roots of polynomial functions. In order to determine if a value is a root of the function, you must make a reasonable guess, and then apply synthetic division to determine if the remainder of the division is 0. If so, then you have found a root.
Formal versus Informal Reasoning
Formal reasoning, also called deductive reasoning, starts with premises that are known to be true and continues towards a logical conclusion.
For example, humans breathe air. David is a human; therefore, David breathes air.
Informal reasoning, also called inductive reasoning, starts with specific observations and combines them to make broad generalizations.
For example, you notice that Julia shows up late to work. Julia is a teenager; therefore, you conclude that teenagers are irresponsible.
Conclusions reached using inductive reasoning can be wrong sometimes, but this type of reasoning is still important. Inductive reasoning is most often used to form hypotheses, which can then be tested using the scientific method.
Mathematics Learning, Instruction, and Assessment

The Mathematics Learning, Instruction, and Assessment domain has about 10 questions. These questions account for 10% of the entire exam.
This domain can be neatly divided into 2 competencies:
- Mathematics Learning and Instruction
- Mathematics Assessment
Let’s talk about some concepts.
Inquiry-Based Learning
Inquiry-based learning is about sparking a student’s curiosity through exploration and discovery. This kind of learning is not instructor-led; instead, the teacher helps facilitate learning by careful scaffolding.In mathematics, this might look like working in small groups to explore a problem and share ideas with one another, or it might involve the teacher posing a problem and the entire class brainstorming together to come up with a solution.For example, the teacher might present the diagram below and ask the students to make their own observations and pose their own questions about the figures.
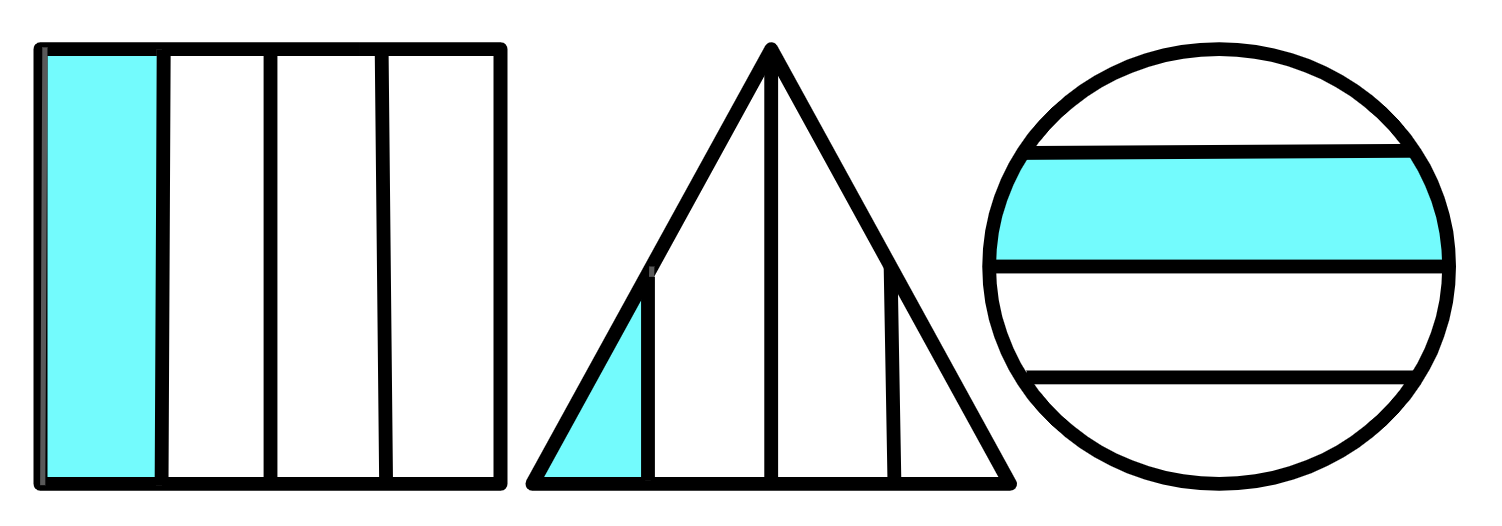
Students may ask questions like:“What fraction of each of the shapes is shaded?” “How can you find the area of each of the shaded regions?” “Is the triangle equilateral?” The teacher can use scaffolding strategies and give students hints (if needed) to help answer these questions and others.
Formative versus Summative Assessments
Formative assessment is given regularly throughout the school year to provide ongoing feedback and help teachers determine concepts that need to be covered in more detail. Formative assessments also help students identify where their own understanding can be improved. Formative assessment is usually lower stakes and can include very informal tasks such as games, projects, and group work, as well as writing a summary about the main point of the lesson that day or submitting an outline of a paper before writing it.
Summative assessments are usually given at the end of a chapter, unit, or course to determine how much the student has learned and retained. These types of assessments are usually higher stakes and include tests, quizzes, final papers, and cumulative projects.
And that’s some basic info about the TExES Math 7-12 exam.
