FTCE Math 5-9 Competencies
Overview
The exam has ten competencies:
- Problem-Solving and Reasoning (13%)
- Manipulatives, Models, and Instructional Technology (6%)
- Assessment in Mathematics (9%)
- Connections Among Mathematical Concepts (7%)
- Number Sense, Operations, and Proportionality (9%)
- Foundations of Algebra (14%)
- Algebraic Thinking (11%)
- Data Analysis, Statistics, and Probability (7%)
- Two-Dimensional Geometry (15%)
- Measurement and Spatial Sense (9%)
So, let’s talk about Problem-Solving and Reasoning first.
Problem-Solving and Reasoning
This competency includes about 10 multiple-choice questions, which makes up about 13% of the entire exam.
These questions test your knowledge of problem-solving strategies and mathematical expressions, as well as your ability to use logic and reasoning.
Let’s talk about some concepts that you will more than likely see on the test.
Teaching Strategies: Problem-Solving
One strategy for helping middle schoolers problem solve, particularly with word problems, is to have them break up the problem into the following steps:
- Write down the information that you know.
- Write down what you need.
- Draw any relevant diagrams.
- Use what you have to work toward what you need.
- Circle the solution. Make sure that you answered the question that was asked and that you have the correct units.
Another problem-solving strategy that helps students find key information in the problem is called C.U.B.E.S:
C ircle the important numbers
U nderline the question statement
B ox the keywords
E liminate extra information
S how work
Deductive versus Inductive Reasoning
Deductive reasoning, sometimes called top-down reasoning, starts with premises that are known to be true and continues towards a logical conclusion.
For example, humans breathe air. David is a human; therefore, David breathes air.
Inductive reasoning, sometimes called bottom-up reasoning, starts with specific observations and combines them to make broad generalizations.
For example, you notice that Julia shows up late to work. Julia is a teenager; therefore, you conclude that teenagers are irresponsible.
Conclusions reached using inductive reasoning can be wrong sometimes, but this type of reasoning is still important. Inductive reasoning is most often used to form hypotheses, which can then be tested using the scientific method.
Manipulatives, Models, and Instructional Technology
This competency includes about 5 multiple-choice questions, which makes up about 6% of the entire exam.
These questions test your knowledge of manipulatives, technology, and multiple representations of mathematical concepts.
Here are some concepts that you may see on the test.
Using Models
Models provide visual pictures of mathematical concepts, which can help to remember concepts, as well as understand them better.
For example, below is a model for squaring the binomial expression 5 x – 3:

Graphing Calculators
In the middle grades, graphing calculators are useful for graphing linear and quadratic equations. They are particularly helpful for students to check their work, once they understand how to graph these kinds of equations by hand.
A graphing calculator can also be used to quickly find statistical measurements from a list of data using the list feature, including minimum, maximum, mean, median, and upper and lower quartiles. This can be helpful in analyzing data from a probability simulation.
Graphing calculators are most helpful when they are not relied on as a crutch for not understanding mathematical concepts. As such, they should be used on a limited basis.
One of the easiest ways to teach students how to use a graphing calculator is to use an online calculator simulator so that they can follow along as you press buttons in sequence on an overhead screen or projector.
Assessment
This competency includes about 7 multiple-choice questions, which makes up about 9% of the entire exam.
These questions test your knowledge of diagnosing students’ needs, interpreting performance, and determining appropriate assessments.
Let’s talk about some specific concepts you need to know.
Formative versus Summative Assessments
Formative assessment is given regularly throughout the school year to provide ongoing feedback and help teachers determine concepts that need to be covered in more detail. Formative assessments also help students identify where their own understanding can be improved. Formative assessment is usually lower stakes and can include very informal tasks such as games, projects, and group work, as well as writing a summary about the main point of the lesson that day or submitting an outline of a paper before writing it.
Summative assessments are usually given at the end of a chapter, unit, or course to determine how much the student has learned and retained. These types of assessments are usually higher stakes and include tests, quizzes, final papers, or cumulative projects.
Audience-Response Systems
Audience-response systems are technology that allows the teacher to poll a large group of students very quickly. They usually involve some kind of handheld voting instrument that is given to each student. Then the students vote on a topic and the results are summarized and sent to the teacher.
For example, the teacher can put a multiple-choice question on the board and ask the students to select a, b, c, or d. After the students make their choices, the teacher can then determine within seconds whether the concept is understood by the majority of students or if the concept needs to be covered more thoroughly.
Connections Among Mathematical Concepts
This competency includes about 5 multiple-choice questions, which makes up about 7% of the entire exam.
These questions test your knowledge of mathematical errors, relationships between skills, and common misconceptions.
Let’s take a look at a concept that will more than likely appear on the test.
Common Misconceptions in Mathematics
Students often confuse area and perimeter, especially when given a shape other than a rectangle. They try to find the area of the figure by adding the lengths of the sides together.
When working with box plots, one common misconception is that the median shown is actually the average value or mean of the data.
Another common misconception is to think that when taking the square root of both sides of an equation, you only get the positive root. It is very easy for students to forget to include both the positive and negative root even after they have been explicitly taught to.
Number Sense, Operations, and Proportionality
This competency includes about 7 multiple-choice questions, which makes up about 9% of the entire exam.
These questions test your knowledge of estimation, factorization, ratios, and relative size.
Here are some concepts that you may see on the test.
Cube Roots
The cube root of a number is the value that when multiplied by itself 3 times, gives you that number.
For example, the cube root of 64 is 4 since 4*4*4 = 64.
The cube root of -729 is -9 since -9*-9*-9 = -729.
Cube roots are not always integers. For example, the cube root of 21 is not an integer since it can only be factored as 1*21 or 3*7. However, we can say that the cube root of 21 is approximately 2.7589…
GCF and LCM
The GCF (Greatest Common Factor) is the largest factor in common for two numbers.
For example, let’s find the GCF of 18 and 108:
First, find all the factors of each number.
18 has factors 1, 2, 3, 6, 9, 18.
108 has factors 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108.
The factors in common between these numbers are 1, 2, 3, 6, 9, and 18.
The largest of these factors is 18; therefore, the GCF of 18 and 108 is 18.
The LCM (Least Common Multiple) is the smallest value that is a common multiple of two numbers.
For example, let’s find the LCM of 6 and 15:
First, list the multiples of each number.
*NOTE: As a rule of thumb, if you are not sure when to stop listing, keep going until you reach the product of the two numbers (in this case 6*15 = 90). This number is always a common multiple of the two; however, it may not be the least common multiple.*
The multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, …
The multiples of 15 are 15, 30, 45, 60, 75, 90, …
30, 60, and 90 are all common multiples of 6 and 15; however, since 30 is the smallest, it is the LCM.
Foundations of Algebra
This competency includes about 11 multiple-choice questions, which makes up about 14% of the entire exam.
These questions test your knowledge of patterns, inequalities, linear equations, and square roots, as well as your ability to simplify expressions.
Let’s talk about some concepts that you will more than likely see on the test.
Solving Inequalities
Example 1:
Solve the inequality 4 x < 2 x + 8.
Isolate x by collecting all of the terms with a variable on one side of the inequality. To do this, subtract 2 x from both sides:
4 x – 2 x < 8
2 x < 8
x < 4

Example 2
: Solve the inequality below:
-7 x + 10 ≤ 31
To solve this inequality, again we need to isolate the variable x . Subtract 10 from both sides:
-7 x ≤ 31 – 10
-7 x ≤ 21
Divide both sides by -7:
x ≥ -3
*NOTE: When you multiply or divide an inequality by a negative number, you must reverse the inequality (flip the sign).*
We can represent the solution x ≥ -3 on a number line. Since this inequality uses the symbol “≥,” the solution includes the value -3 and everything greater than -3. So, we shade to the right of -3 on the number line:

Determining the Equation of a Line
The equation of a line can be determined using two points on the line or with the y -intercept and slope of the line.
This information can be plugged into various forms of linear equations:
Point-Slope Form
:
y-y1=m(x-x1)
where m is the slope and (x1,y1) is a point on the line.
Slope-Intercept Form
: y = mx + b where m is the slope and b is the y -coordinate of the y -intercept.
The slope of a line is calculated using the formula
m = (y2–y1)/(x2–x1).
Example 1: You are given the graph below.
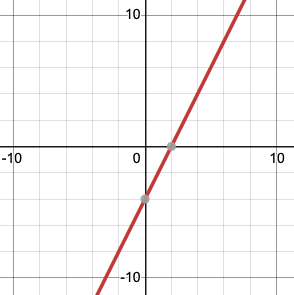
The slope can be calculated using any two points on the line. We will choose (2, 0) and (0 , -4):
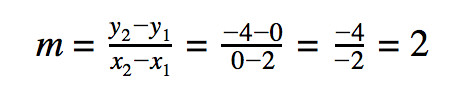
Using the point-slope form of an equation of a line, y – 0 = 2( x – 2).
Example 2: Given that a line has a slope of -8 and a y -intercept at (0, 4), find the equation of the line.
In this case, it is easier to find the equation of the line in slope-intercept form. We know that m = -8 and b = 4. Therefore, y = mx + b = -8 x + 4. The equation of the line is y = -8 x + 4.
Algebraic Thinking
This competency includes about 8 multiple-choice questions, which makes up about 11% of the entire exam.
These questions test your knowledge of solving systems of equations and quadratic functions, as well as finding zeros of polynomials. You also need to know the laws of exponents.
Here are some concepts you need to know.
Factoring Polynomials
Factoring is writing a polynomial as the product of two other polynomials. This is usually applied to simplify an expression involving polynomials or to find the roots of a polynomial. There are many strategies for factoring polynomials including factoring out the greatest common multiple, factoring perfect square trinomials, factoring by grouping, and several other strategies.
Let’s take a look at some examples.

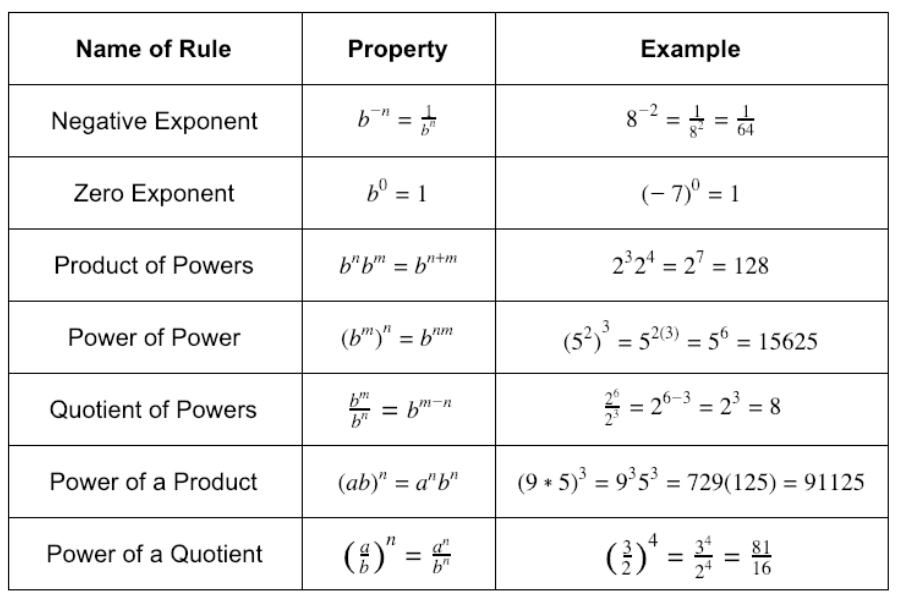
Laws of Exponents
For a (any real number), b (any non-zero real number), and n and m (natural numbers), the following properties are true:
Data Analysis, Statistics, and Probability
This competency includes about 5 multiple-choice questions, which makes up about 7% of the entire exam.
These questions test your knowledge of statistical measures, graphical representations of data sets, population samples, and probabilities.
Let’s talk about a concept that you will more than likely see on the test.
Central Tendency
Measures of central tendency help us to determine how data is distributed by identifying a single value at roughly the center of the data. We will consider several measures of central tendency below.
The mean of a data set is the average value of a data set. This can be found by adding together all of the values and dividing by the total number of values.
The mode of a data set is the value that occurs most frequently in the data set. It is possible to have more than one mode in a data set if several values occur the most.
The median of a data set is the middle value in the set when the data points are ordered least to greatest If there is an even number of data points, there will not be an exact middle. In this case, the median is found by taking the average of the two data points closest to the middle.
For example, suppose that the ages for a group of ten students were collected and are listed below:
9, 11, 13, 11, 8, 7, 13, 9, 9, 12
The mean of this data set can be found by adding all of these ages together and dividing by 10 since there are 10 students:
Mean = (9+11+13+11+8+7+13+9+9+12) /10=10.2
To find the mode and median of a data set, it is helpful to reorder the set from lowest to highest.
7, 8, 9, 9, 9, 11, 11, 12, 13, 13
Now we can see that the mode of the data set is 9, since 9 occurs 3 times, which is more than any other data point.
Since the data set has an even number of values, there are two values in the middle: 9 and 11. To find the median, you must average 9 and 11; therefore, the median of the data set is 10.
Two-Dimensional Geometry
This competency includes about 11 multiple-choice questions, which makes up about 15% of the entire exam.
These questions test your knowledge of geometric figures such as triangles, quadrilaterals, angles, and circles, including relevant theorems, as well as the coordinate plane.
The following concept is likely to pop up on the test.
Trigonometric Ratios
There are 6 trigonometric ratios that you should know:

When given x, an angle measure in a right triangle, and two of the sides, opposite and adjacent to the angle or the hypotenuse, this provides the information needed to find the length of the missing side.
Example 1
: Find the hypotenuse of the triangle below.
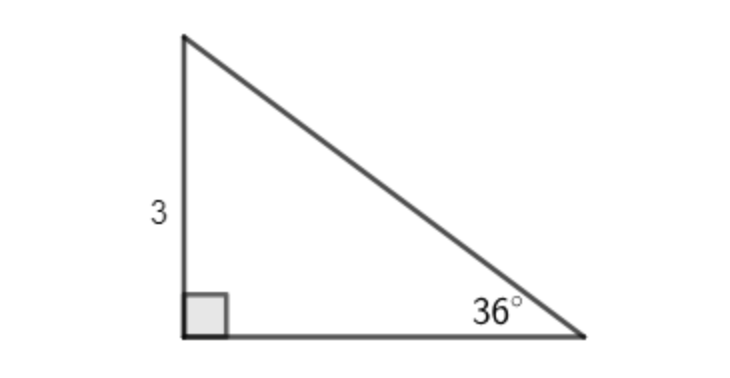
First, consider which trigonometric identity is appropriate to use. Here we are given an angle and the opposite side, and we would like to know the hypotenuse. The appropriate trig identity is therefore the sine function, since it involves the opposite side and the hypotenuse:
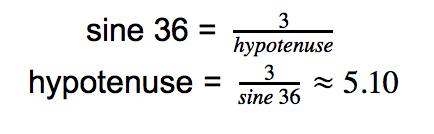
Example 2
: Find the missing angle x , of the right triangle, if you know that cotangent x = 6.

Now, to solve for the angle x , we need to use the inverse tangent function:
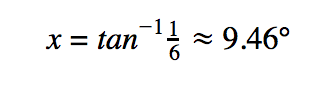
*NOTE: If you are working in degrees, make sure your calculator is in degree mode when using trigonometric functions.*
Measurement and Spatial Sense
This competency includes about 7 multiple-choice questions, which makes up about 9% of the entire exam.
These questions test your knowledge of three-dimensional figures, area, and volume, as well as your ability to convert between units.
Let’s talk about some concepts that you will more than likely see on the test.
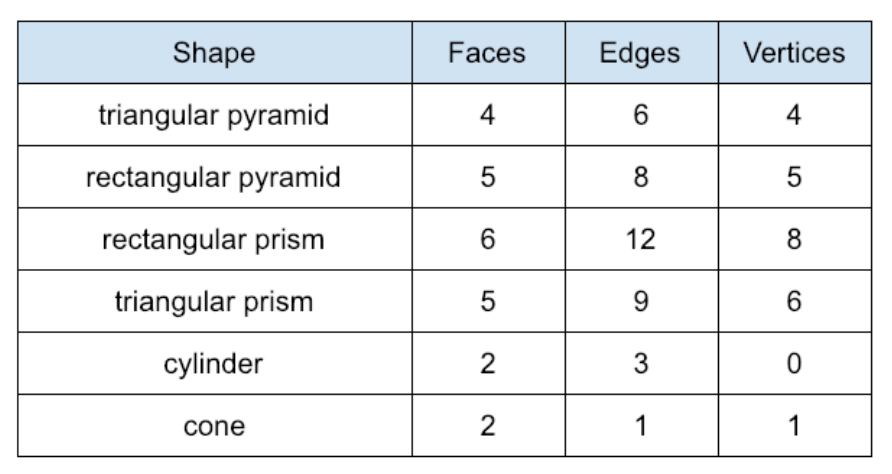
Characteristics of Three-Dimensional Figures
When looking at three-dimensional figures, it can be helpful to identify the different parts of the figure. A face of a three-dimensional figure is a flat surface. An edge
is the line where two faces meet. A vertex is the point where three faces meet.
Below is a table of shapes and the number of faces, edges, and vertices each shape has.
Identifying Nets
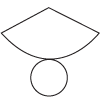
A net of a three-dimensional figure is a two-dimensional representation of the shape that can be folded into the three-dimensional figure by the faces along the edges.
Here are some tips for identifying which net matches with a given 3D shape:
- Make sure that the net has the correct number of faces.
- If you are having trouble visualizing what the shape looks like folded, cut out the net and actually try folding it up.
- Consider what shapes the faces of the 3D shapes are. For example, in a cylinder, we know that two of the faces are circles and one is a rectangle. This means that the net has to contain two circles and a rectangle.
Here is the net of a cone:
And that’s some basic info about the FTCE Middle Grades Mathematics 5-9 exam.
